第2节 晶体的宏观对称(6)

    2.2.3对称要素的组合

   在晶体的对称中，可以有一个对称要素单独存在，也可以有几个对称要素组合在一起共同存在。但对称要素的组合不是任意的，它服从“对称要素组合定理”的规律。
   定理一: 如有一偶次对称轴Lⁿ与对称中心共存，则过C且垂直于此Lⁿ的平面，必为一对称面（图2-27）。
   简式为： L^n（偶）×C = L^n（偶）PC（L^n（偶）⊥P）
   [逆定理一] 若有一偶次对称轴Lⁿ垂直于对称面P，二者的交点必为对称中心C。
    简式为：? L^n（偶）×P = L^n（偶）PC（L^n（偶）⊥P）
   [逆定理二] 若有一对称面P和对称中心组合，必存在一个垂直于对称面的偶次对称轴。
   简式为： P×C = L^n（偶）PC（L^n（偶）⊥P）
    定理二? 如果有一个二次对称轴L²垂直Lⁿ，则必有n个L²垂直Lⁿ，且任意两相邻L²间的夹角δ=360°／2n（图2-28）。
    简式为： Lⁿ×L² = LⁿnL²（Lⁿ⊥L²）
   [逆定理] 如有两个L²以δ角相交，则过两者交点之公共垂线必为一n次对称轴且n =360°／2δ。

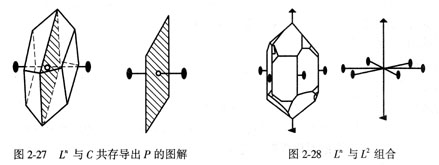
   定理三: 若有一个对称面P包含Lⁿ，则必有n个对称面包含Lⁿ，且任意两相邻对称面间的夹角δ=360°／2n (图2-29)。
    简式为： Lⁿ×P→LⁿnP（Lⁿ∥P）
    [逆定理]? 如有两个P以δ角相交，则两者交线必为一个n次对称轴且轴次n =360°／2 δ。
   定理四: 如有一个对称面P包含L_iⁿ (或有一个L²垂直L_iⁿ )，当n为偶数时，则必有n／2个P包含L_iⁿ和n／2个L²垂直L_iⁿ；当n为奇数时，则必有n个P包含L_iⁿ和n个L²垂直L_iⁿ，且对称面P的法线与相邻L²间的夹角δ均为360°／2n (图2-30)。

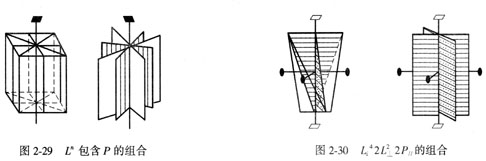
    简式为：
       L_iⁿ×P_// = L_iⁿ×L_⊥² = L_i^n? L_⊥²? P_//（n为偶数）
       L_iⁿ×P_// = L_iⁿ×L_⊥² = L_iⁿ nL_⊥² n P_//（n为奇数）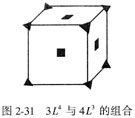
    [逆定理] 如有—个L²与一个P斜交，P的法线与L²的交角为δ，则垂直于L²且包含P的直线必为一个n次倒转轴L_iⁿ ，n=360°／2δ。
    定理五? 若Lⁿ与L^m以δ角斜交，则围绕Lⁿ必有共点且对称分布的n个L^m ，围绕L^m必有共点且对称分布的m个Lⁿ，而且任意两相邻的Lⁿ与L^m之间交角均为δ(图2-31)。
    简式为：? Lⁿ×L^m = nL^mmLⁿ（Lⁿ与L^m斜交）