| 第2节 晶体的宏观对称(3)
(4)旋转反伸轴(倒转轴)Lin
旋转反伸轴是过晶体中心的一假想直线,晶体绕此直线旋转一定角度,再对晶体中心进行反伸操作,可使相等部分重复出现,以Lin表示。
倒转轴的对称操作是旋转加反伸,其轴次同样遵守晶体对称规律,即也只有Li1、Li2、Li3、Li4、Li6五种。倒转轴的图解说明示于图2-14。
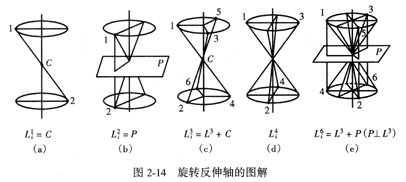
Li1的对称操作为旋转360°后反伸,其与单一的反伸等效,即Li1 = C(图2-14a)。
Li2的对称操作为旋转180°后反伸,如图2-14b。初始点1绕Li2旋转180°后,经过C的反伸与点2重合,点2再旋转180°后反伸于点1复原。由b图可看出,点1和点2可以通过垂直Li2的对称面反映得到,即二次倒转轴等效于垂直它的对称面,即Li2 = P。
Li3的对称操作为旋转120°后反伸,如图2-14c。点1经过Li3的操作可依次得到2、3、4、5、6并还原至点1。如果用L3和C代替Li3进行对称操作,点1通过L3操作可得到点1、3、5,再经过C操作又得到点2、4、6,这与由Li3的操作等效,所以三次倒转轴可表示为Li3 = L3+C。
Li4的对称操作为旋转90°后反伸,如图2-14d。点1经过Li4的操作可依次得到2、3、4并还原至点1。Li4不能用其它对称要素或它们的组合来间接表达,是一个独立的对称要素。
Li6的对称操作为旋转60°后反伸,如图2-14e。从点1开始,按旋转60°后反伸操作得点2、3、4、5、6,并由点6返回到点1复原。若用L3和P代替Li6进行对称操作,由点1开始,经L3操作可得到点1、3、5,再经过垂直L3的P操作又可得到点2、4、6,其结果与由Li6操作的完全相同,因而六次倒转轴可以表示为Li6 = L3 + P (P⊥L3)。
旋转反伸轴一般常用的为Li4和Li6,Li4是一个独立的对称要素,而Li6虽有Li6 = L3 + P的等效组合表达,但由于提高了轴次,习惯上应用Li6。
(5)旋转反映轴(映转轴)Lsn
旋转反映轴是过晶体中心的一假想直线,晶体绕此直线旋转一定角度后,再对过晶体中心且垂直此直线的平面反映,可使晶体相等部分重复,以Lsn表示。
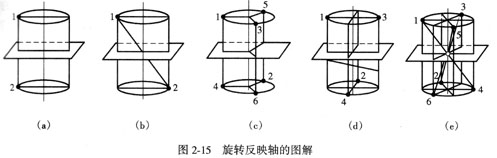
映转轴的对称操作为旋转加反映。也只有Ls1、Ls2、Ls3、Ls4、Ls6五种(见图2-15)。旋转反映轴没有独立表达的对称要素产生,其五种对称要素均可用其它要素间接表示:
Ls1 = P = Li2,? Ls2 = C = Li1,? Ls3 = L3 + P = Li6,? Ls4 = Li4,? Ls6 = L3+C = Li3。
|

