| 第2节 晶体的宏观对称(5)
(2)对称要素的极射赤平投影
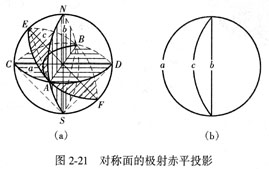
①对称面的投影:将对称面扩展与投影球相交,所得球面上的大圆有如下几种(图2-21(a)):
水平对称面的投影与基圆重合(图2-21(b)中a);
直立对称面的投影为通过基圆中心的直线(图2-21(b)中b);
倾斜面的投影是以基圆直径为弦的大圆弧(图2-21(b)中c,只表示上半球投影)。
②对称轴的投影:将轴线延长与投影球相交,所得两点称为该轴在球面上的出露点,其投影分为:
水平的对称轴投影在基圆的圆周上(图2-22a);
直立的对称轴投影在基圆的中心(图2-22b);
倾斜的对称轴投影在基圆的圆周内(图2-22 c)。
对称轴L2、L3、L4、L6在投影图上分别以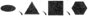 表示。 表示。
③对称中心的投影:是在投影图中心以一个小○表示(图2-23)。
(3)吴氏网(Wulff Net)的构成及应用
 ①吴氏网的构成: 图2-24示出吴氏网。网面相当于极射赤平投影面,目视点投影于网中心,圆周为基圆,两个直径是相互垂直且垂直于投影面的直立大圆的投影,大圆弧相当于球面上倾斜大圆的投影,小圆相当于球面上垂直投影面的直立小圆的投影。吴氏网可以用作球面坐标的量角规:基圆上的刻度可度量方位角φ,直径上的刻度可以度量极距角ρ,应用大圆弧上的刻度可以度量晶面的面角。 ①吴氏网的构成: 图2-24示出吴氏网。网面相当于极射赤平投影面,目视点投影于网中心,圆周为基圆,两个直径是相互垂直且垂直于投影面的直立大圆的投影,大圆弧相当于球面上倾斜大圆的投影,小圆相当于球面上垂直投影面的直立小圆的投影。吴氏网可以用作球面坐标的量角规:基圆上的刻度可度量方位角φ,直径上的刻度可以度量极距角ρ,应用大圆弧上的刻度可以度量晶面的面角。
②吴氏网的应用:用一张透明纸覆盖于网面上,描出基圆,用×标出网中心。选择零度子午面,其与基圆的交点为φ= 0°。现举例说明网面投影的应用:
作晶面M( ρ1,?φ1)的极射赤平投影(图2-25)。在基圆φ=0°点顺时针数一角度φ1,交于基圆上一点,作该点与网中心点的连线,该连线为方位角φ1的子午面的投影(M点在此线上),M点与网中心的距离即为ρ1。由于在这一方向上未给出直立大圆(子午线),必须旋转透明纸(保持中心点不变),使纸上的直线与网的水平半径重合,利用水平半径上的刻度,从网中心开始量得角度φ1,并在水平半径上交于一点M,M点就是该晶面的极射赤平投影点。
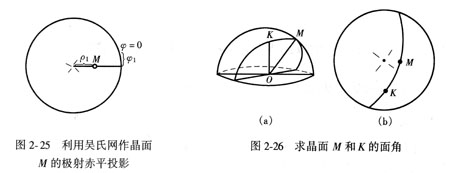
已知晶面的球面坐标M(ρ1,φ1)和K(ρ2,φ2),求此二晶面的面角。如图2-26(a)所示,M和K分别是该两晶面的极点,OM和OK是两晶面的法线,两晶面的面角为其法线间角,即M、K点所在的大圆弧上MK点间的弧角。中心不动旋转透明纸,使M和K点落于吴氏网的一条大圆弧上,读得M与K间的刻度,即为M与K两晶面的面角(图2-26(b))。
|

