第2节 晶体的宏观对称(2)

    （2）对称轴Lⁿ
    对称轴是通过晶体中心的一条假想直线，当晶体绕此直线旋转一定角度后，可使相等部分重复出现，记为Lⁿ。
    对称轴的对称操作是绕直线的旋转。旋转一周重复的次数称为轴次n， 重复时所旋转的最小角度称为基转角α。轴次与基转角间的关系为 n= 360°／α。
    晶体对称研究表明，实际晶体中可以存在的对称轴仅有L¹、L²、L³、L⁴、L⁶五种。一次对称轴L¹没有实际意义，因为任何晶体旋转360°都可以复原。五次对称轴（L⁵）和高于六次的对称轴（L⁷、L⁸……）均不允许存在，这一规律称为晶体的对称规律。轴次高于2的对称轴L³、L⁴、L⁶称高次轴。
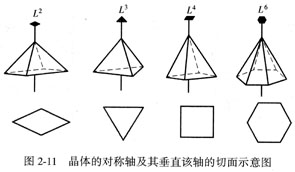
    图2-11示出的是对称轴L²、L³、L⁴和L⁶的基本几何图形。晶体中允许没有对称轴，也可以有一种或几种对称轴同时存在。在书写时，对称轴的数目写在对称轴符号的前面，如三个四次轴记3L⁴。

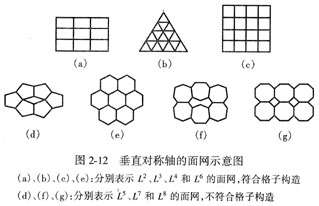
    晶体的对称规律表明，在空间格子中，垂直于对称轴必须有符合该对称轴特征的面网存在。从图2-12可以看出，有对称轴L²、L³、L⁴、L⁶存在的面网，能够无间隙地布满整个平面，构成空间格子面网（图中 a、b、c、e）。而围绕L⁵、L⁷、L⁸所形成的面网，不能无间隙地布满整个平面（图中 d、f、g），违背了空间格子的构造规律，这就是不允许存在五次及高于六次对称轴的原因。

（3）对称中心C
    对称中心是晶体中心的一个假想定点，过此点的任意直线的等距离两端，可以找到晶体的相同部分。其对称操作是以此点为中心的反伸（倒反），符号用C表示。
    如图2-13所示，C点为对称中心，在图形上任取一点A与C联线，再由C点反向延伸至等距离处，能找到对应点A^，。同样，B和B^，也是通过C点反伸的对应点。晶体中可以没有对称中心，或者仅有一个对称中心。晶体中如果有对称中心，晶体上必然存在两两平行且反向相等的晶面。