| 第5节 晶体构造的几何理论(6)
2.5.5点群和空间群的符号
(1)点群的国际符号
点群国际符号的表达只使用三类对称要素(对称轴、对称面、旋转反伸轴),其它对称要素做间接表达,这三类对称要素的国际符号为:
对称面: 以m表示;
对称轴: 以轴次的数字表示,如1、2、3、4和6;
倒转轴: 在轴次的数字上加“-”号,如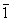 (C)、m( (C)、m(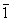 )、 )、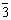 、 、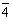 和 和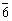 。 。
点群的国际符号是由规定方向(不超过三个)上存在的对称要素构成,按规定方向的顺序依次排列表达相应观察方向上所存在的对称要素。表2-9列出了7个晶系所规定的各个观察方向,图2-58示出了各观察方向的空间方位。
.jpg)
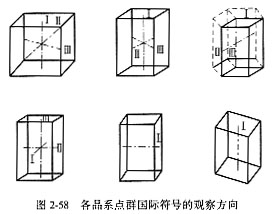
由点群L44L25PC导出国际符号:L44L25PC属于四方晶系,其国际符号规定的观察方向是:co、ao、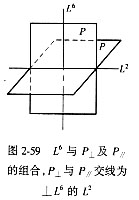 (a0+bo)。co方向(Z轴)上存在的对称要素有一个L4和垂直此L4的对称面P,因此第一位写做4/m; ao方向(X轴)上存在的对称要素有一个L2和垂直此L2的对称面P,因此第二位写做2/m; (ao+bo)方向(X轴与Y轴平分线)上的对称要素有一个L2和垂直此L2的对称面P,所以第三位写作2/m;于是L44L25PC的国际符号应写为 (a0+bo)。co方向(Z轴)上存在的对称要素有一个L4和垂直此L4的对称面P,因此第一位写做4/m; ao方向(X轴)上存在的对称要素有一个L2和垂直此L2的对称面P,因此第二位写做2/m; (ao+bo)方向(X轴与Y轴平分线)上的对称要素有一个L2和垂直此L2的对称面P,所以第三位写作2/m;于是L44L25PC的国际符号应写为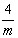 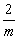 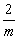 ,进一步简化为 ,进一步简化为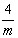 mm。显然根据组合定理可由该符号推导出所有的其它对称要素。 mm。显然根据组合定理可由该符号推导出所有的其它对称要素。
由国际符号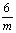 mm导出点群:首位6表示出六方晶系,其国际符号的三个观察方向为c0、a0、(2a0+b0),相应对称要素是c0方向有一个L6和垂直L6的P,有L6×P⊥→ L6P⊥C;a0方向有一个平行L6的P,有L6×P// → L66P//;包含L6的P与垂直L6的P的交线必为垂直于L6的L2(图2-59),又有L6×L⊥2→ L66L⊥2;最后将所有的对称要素组合在一起,便得到点群L66L27PC。 mm导出点群:首位6表示出六方晶系,其国际符号的三个观察方向为c0、a0、(2a0+b0),相应对称要素是c0方向有一个L6和垂直L6的P,有L6×P⊥→ L6P⊥C;a0方向有一个平行L6的P,有L6×P// → L66P//;包含L6的P与垂直L6的P的交线必为垂直于L6的L2(图2-59),又有L6×L⊥2→ L66L⊥2;最后将所有的对称要素组合在一起,便得到点群L66L27PC。
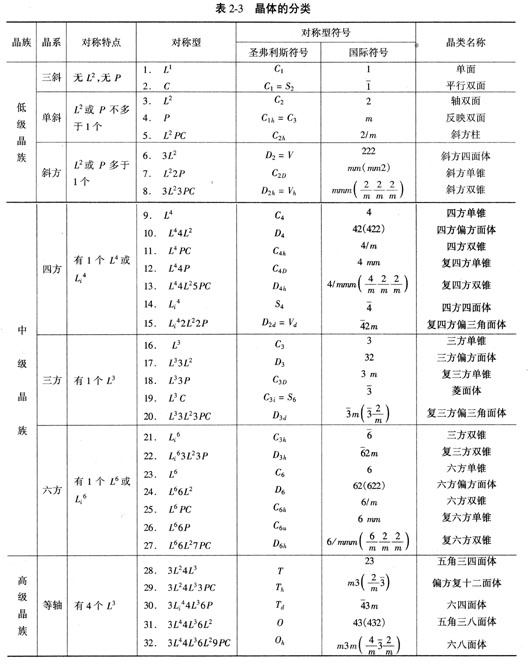
32种点群的国际符号见表2-3所列。
(2) 点群的圣弗利斯符号
圣弗利斯符号是根据对称要素组合的几种基本规律,用不同字母来表示对称型中对称要素的基本组合而写出的,具体说明如下:
Cn —— 表示Ln单独存在,如L1、L2、L3、L4、L6分别以C1、C2、C3、C4、C6表示。
Cnh—— 表示Ln×P⊥→ LnP(C),如P、L2PC、L3P(Li6)、L4PC、L6PC分别以C1h、C2h、C3h、C4h、C6h表示。
Cnv—— 表示Ln×P// → LnnP//,如L22p、L33P、L44P、L66P分别以C2v、C3v、C4v、C6v表示。
Dn—— 表示Ln×L⊥2 → LnnL2,如3L2、L33L2、L44L2、L66L2分别以D2、D3、D4、D6表示。
Dnh—— 表示Ln×L2⊥×P⊥ → LnnL2(n+1)P(C),如3L23PC、L33L24P(Li63L23P)、L44L25PC、L66L27PC分别以D2h、D3h、D4h、D6h表示。
Dnd—— 表示对称面不包含L2,而是处于平分L2夹角的位置上,如Li42L22P、L33L23PC分别以D2d、D3d表示。
i或Ci —— 表示倒转轴,如Ci = Li1 = C、C3i = Li3 = L3C。
S或Cs—— 表示映转轴,如Cs = Ls1 = P、S2 = Ls2 = C、S4=Ls4=Li4、S6=L3C=C3i。
此外,D2又以V表示,即V = D2、Vh=D2h、Vd=D2d。
T —— 表示等轴晶系对称型3L24L3的组合。
Th-- 表示3L24L3中加入水平对称面获得的3L24L33PC。
Td-- 表示3L24L3中加入平分L2夹角方向的对称面获得的3Li44L36P。
O —— 表示等轴晶系对称型3L44L36L2的组合。
Oh-- 表示3L44L36L2中加入水平对称面获得的3L44L36L29PC。
32种对称型的圣弗利斯符号见表2-3。 |

