第5节 晶体构造的几何理论(1)

     2.5.1布拉维格子

    (1) 单位平行六面体的划分
    我们已经知道，晶体构造就是单位平行六面体在三维空间作无间隙地堆叠或穿插组合。在研究格子构造中，这种单位平行六面体的划分要求遵循下列原则：
    ① 应能反映整个结点分布所具有的对称性；
    ② 棱间的直角最多；
    ③ 体积最小。
    图2-45是具有L⁴4P对称的格子，图中标出了6种选择方式。显然3、4、5、6四种划分方法都与L⁴4P的对称不符，在剩下的1、2方式中，都满足选取原则①、②，但以1的体积最小，故应选取1作为单位平行六面体。
    单位平行六面体三根棱长a、b、c及其夹角α、β、γ称为单位平行六面体的晶格常数。

（2）七个晶系单位平行六面体及格子类型
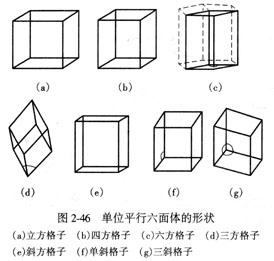
    按照上述单位平行六面体的划分原则，对7个晶系的晶体进行划分，得到了七个晶系单位平行六面体的晶格常数特征(图2-46)：
    立方格子：a = b = c, α=β=γ= 90°；   四方格子： a =b ≠c, α=β=γ= 90°；
     六方格子：a =b ≠c, α=β= 90°, γ=120°；  三方格子： a = b = c, α=β=γ≠90°；
     斜方格子：a ≠b ≠c, α=β=γ= 90°；   单斜格子： a≠b≠c, α=γ= 90°, β≠90°；
     三斜格子：a ≠b ≠c, α≠β≠γ≠90°；
   显然，单位平行六面体晶格常数与晶体外形研究中给出的晶体常数是一致的。

    对单位平行六面体进行附加结点的分析，按分布方式可划分出格子的基本类型(图2-47)：

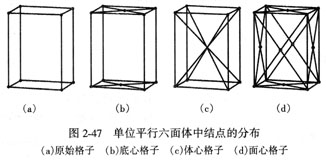
    原始格子(P)：结点分布于单位平行六面体的角顶。其中三方菱面体格子用符号R表示；
    底心格子(C)：结点分布于单位平行六面体的角顶和一对面的面心。如果是(100)或(010)面中心有结点时，则分别用符号A和B表示，称为侧面心格子，或称A格子，B格子；
    体心格子(I)： 结点分布于单位平行六面体的角顶和体中心；
    面心格子(F)：结点分布于单位平行六面体的角顶和各面的中心。