8.5 相图热力学基本原理(5)

第8章相平衡与相图

                  8.5 相图热力学基本原理(5)

     8.5.4 从自由能-组成曲线推导相图举例

        当体系中各可能出现的相在不同温度下自由能-组成曲线及其相互位置关系确定之后，便可由此推导出相应于不同温度下相界点的平衡位置。下面简要介绍两个二元系统基本类型相图的推导过程。
        1. 固态部分互溶具有低共熔类型的二元相图
        当组分A和B部分互溶时，固相能形成两种固溶体。此时系统可能存在三个相：液相、α固溶体及β固溶体。当考虑温度取值从T_l到T₆时，三个相的自由能-组成曲线L、α以及β曲线如图8-75（a~f）所示。
        在A的熔点T₆时，α线与L线相切于a点（参见图8-75（a）），因为在此温度下纯A固相与液相两相平衡，自由能相等。其它全部组成范围内，由于L线位于α、β线之下，故只有液相能够稳定存在。
        当温度降至B的熔点T₅时，β线与L线相切于b点（道理同上）。同时，α线一部分位于L线以下并与L线公切于c、d点。图8-75（b）表示了共存的两相分别是组成为c的α相固溶体和组成为d的液相。
        当温度进一步降至T₄时，α、β线均有一部分在L线以下，见图8-75（c），此时存在两条公切线，表示有两对共存的相，即α固溶体和液相平衡以及β固溶体和液相平衡。
        在低共熔点T₃时，α、β和L三条曲线有一条公切线，如图8-75（d）。此时α、β和L三相共存，由于L曲线上切点k位于其它两切点j和i之间，就形成了低共熔类型的相图，k点即为低共熔点。
        当温度继续降低到低共熔点以下如T₂时，L线位于α、β曲线公切线之上，此时L相不稳定，只有α、β相稳定存在，并且在两切点组成之间是α、β相共存。
        最后将各温度下各相自由能-组成曲线间的切点对应地描于温度组成T-x坐标上，便可得到该系统的相图，如图8-75（g）所示。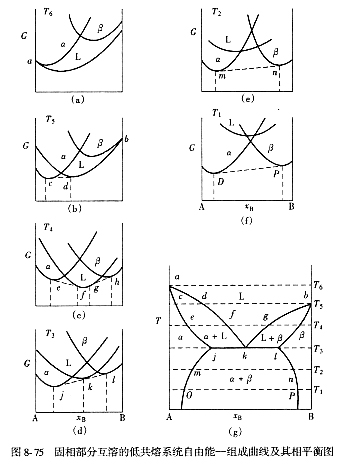

2. 低共熔类型二元系统相图
        假设组成A和B在液态时完全互溶、在固态时完全不溶时，体系将可能存在三个相：液相、A固相和B固相。
        当体系温度低于纯A熔点T₁时，若以液态的纯A和纯B为标准态，体系的液相线L如图8-76（a）所示，纯A固相的自由能（ΔG=-ΔG_fA）位于纵坐标a点。纯B固相自由能（ΔG_B=ΔG_fB）位于b点。此处ΔG_fA、ΔG_fB为纯A、B组成的熔化自由能：

           （8-85）
        通过a点作与L线的切线得切点c，而过b点作直线无法与L线相切。故当x_A<x_C时，体系纯A固相与液相共存，而x_A>x_C时仅存单一液相。
        在低共熔温度T_e时，纯A固相自由能a′点与纯B固相自由能b′点连线与液相线L相切于e点。此时三相共存如图8-76（b）。而当温度低于T_e时，纯固相自由能a、b点连线位于液相线以下，故液相不再存在。其相图示于图8-77。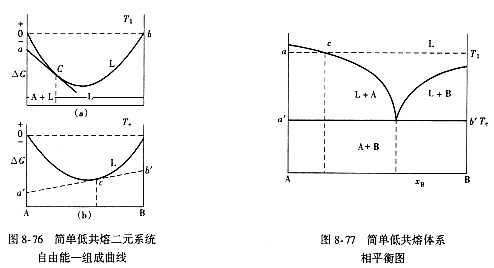

        关于从自由能-组成曲线推导相图可以总结归纳出如下要点：
        ① 体系中每一相都有一条自由能-组成曲线，有一个相应的曲线方程。该相在相图中有对应的位置，在一定温度和压力下可根据它的自由能大小来判断它是否存在。如果它的自由能比其它相的自由能低，则表示它是最稳定的相。
        ② 两条自由能-组成曲线如果不相交，表示在某温度下只有单相稳定存在。这个稳定相就是自由能最低的那个相。在相图中对应的是单相区。
        ③ 两条自由能-组成曲线如果相交，必然存在一条公切线，两个切点相应的组成表示在此温度下两个平衡相的组成点。
        ④ 两条自由能-组成曲线相交，但只在交点相切（即只有一个切点），则在相图中与这个切点相对应的是一个相变点，表示同成分的两个相的相平衡。
        ⑤ 三条自由能-组成曲线依次相交，存在两条公切线，有两对平衡相，切点对应的组成分别表示其平衡相的组成。
        ⑥ 三条自由能-组成曲线只存在一条公切线，表示三相平衡。三个切点对应的组成表示三个平衡相的组成。
（本节完，本章完）

第 [1] [2] [3] [4] 5 页