
 |
第8章 相平衡与相图 |
| 8.5 相图热力学基本原理(1) 8.5.1 相平衡的化学位 根据热力学第二定律,体系在恒温恒压不做非膨胀功的条件下,自由能是判断过程自发进行或是平衡的准则,用始末态自由能之差来判断:ΔG < 0,过程能自发进行;ΔG > 0,过程不能自发进行;ΔG = 0,系统处于平衡状态。 在多元系统中,自由能不仅和温度、压力有关,而且和组元浓度有关,即G = f(T, P, n1, n2, …, ni),ni表示组元i的摩尔数。也就是说恒温恒压下,一定浓度的体系有一定自由能,浓度不同自由能也不同。 系统中组元i的化学位(μi)的定义为:在恒温恒压下,除i物质外其它物质的摩尔数均维持不变(即nj不变)时,系统的自由能随i物质的摩尔数ni的变化率。换句话说,在无限大系统中,在恒温恒压下,每增加1mol i物质引起系统的自由能的变化,定义为系统中组元i的化学位。化学位亦即偏摩尔自由能 式中,nj表示除了i组元外系统中其它所有组元。 1. 图解法求偏摩尔自由能 G为系统自由能,具有容量性质。若系统由i种物质组成,则 G = f(T, P, n1, n2, …, ni) (8-24) 恒温恒压时,dP=0,dT=0,则 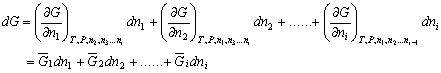 (8-25) (8-25)对二元系统,上式改写成: 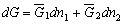 (8-26) (8-26)偏摩尔自由能的总和: 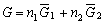 (8-27) (8-27)对上式微分: 比较式(8-26)和式(8-28),可得: 设 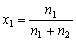 , ,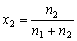 ,把上式改写为: ,把上式改写为: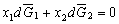 (8-30) (8-30)及 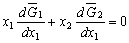 (8-31) (8-31)因为x1+x2=1,dx1=-dx2,则 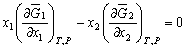 (8-32) (8-32)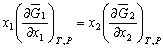 (8-33) (8-33)利用上式可以由一个组元的偏摩尔自由能求得另一组元的偏摩尔自由能。对于一个二元系统,如果用G’表示二元系统的摩尔自由能,则 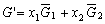 (8-34) (8-34)对上式微分: 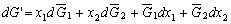 (8-35) (8-35)因为根据式(8-30),有 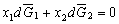 ,所以 ,所以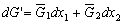 (8-36) (8-36)将上式乘以x1/dx2整理后得: 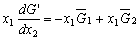 (8-37) (8-37)或 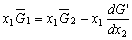 (8-38) (8-38)代入式(8-34),得 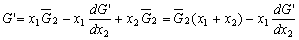 (8-39) (8-39)所以 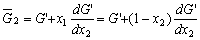 (8-40) (8-40)同样有 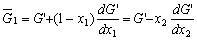 (8-41) (8-41)假设知道G′是组成的函数后,就可以用图解的方法求出 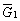 和 和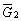 。具体方法如下: 。具体方法如下: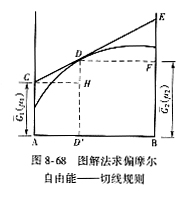 图8-68中曲线表示G′为x2的函数。对一定浓度的溶液D′,其G′值为DD’。在D点作切线交于x2 = 0的纵轴上C点,则AC为 图8-68中曲线表示G′为x2的函数。对一定浓度的溶液D′,其G′值为DD’。在D点作切线交于x2 = 0的纵轴上C点,则AC为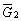 值。这就是偏摩尔自由能的切线规则。证明如下: 值。这就是偏摩尔自由能的切线规则。证明如下:在D点,G′=DD′=BF,由三角形DEF可知切线斜率为EF/(1-x2)。用图中有关数值代入式(8-40),得: 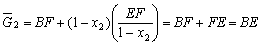 ?(8-42) ?(8-42)因此,切线在x2 = 1的纵坐标上的截距BE为 。同样可得: 因为偏摩尔自由能 |
版权所有 民众工作室.制作 |