
 |
第8章 相平衡与相图 |
| 8.5 相图热力学基本原理(3) 3. 二元固态溶液或液态溶液自由能-组成关系式 若由处于标准状态的纯物质A(摩尔分数为xA)和纯物质B(摩尔分数为xB)混合形成1 mol固态溶液S(xA,xB)或液态溶液L(xA,xB)。 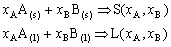 (8-66) (8-66)上述过程自由能的变化ΔGm,称固态溶液或液态溶液生成自由能或混合自由能。根据热力学基本原理,由上述反应得到: 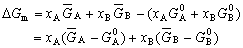 (8-67) (8-67)式中, 代表标准状态下固态或液态纯A和纯B的摩尔自由能, 为固态溶液或液态溶液的偏摩尔自由能,即化学位。在一定温度下 和 可通过组成的活度ai得到联系,表达式如下: 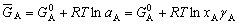 (8-68) (8-68)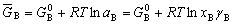 (8-69) (8-69)式中,γA、γB分别为组成A和B的活度系数。 将式(8-68)和(8-69)代入式(8-67),于是得到混合自由能ΔGm的一般关系式: 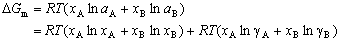 (8-70) (8-70)由此可见,无论是生成二元固态或液态溶液,就混合过程而言其自由能变化ΔGm均具有相同表达式(8-70)。等式右边的第一项表示混合为理想状态时(γA = γB = 1),混合对自由能的贡献,故称之为理想混合自由能ΔGmI;等式右边第二项包含了两种组成的活度系数,表示混合的非理想过程,因此反映了整个溶液体系的不理想程度,常称之为混合过剩自由能ΔGmE。所以实际混合过程的自由能变化ΔGm为理想混合自由能ΔGmI与混合过剩自由能ΔGmE两部分之和: 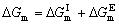 (8-71) (8-71)在一定温度下,若γi>1,则ΔGmE>0,表示体系相对理想状态出现正偏差;反之γi<1则ΔGmE<0,体系出现负偏差。因此,ΔGmE的大小正负直接影响体系自由能-组成曲线的性态。 4. 二元溶液自由能-组成曲线性态 在等温等压条件下,对式(8-71)两边关于xA取微分,并考虑式(8-70)关系得: 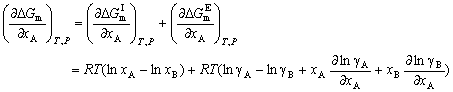 (8-72) (8-72)考虑dxA=-dxB和Gibbs-Duhem公式 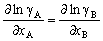 (8-73) (8-73)则式(8-72)可写成: 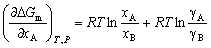 (8-74) (8-74)对上式关于xA再次微分,并再次利用Gibbs-Duhem公式,可得混合自由能关于xA的二阶导数 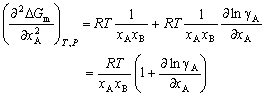 (8-75) (8-75)根据混合自由能关于组成一阶及二阶导数,可分析得出二元溶液自由能-组成曲线的一般性态。 1)两组分端点区域 当混合体系组成点位于两端足够小邻域内,混合体系将成为极稀溶液。此时,混合自由能二阶导数 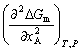 主要决定于 主要决定于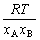 而恒为正值,一阶导数 而恒为正值,一阶导数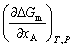 决定于 决定于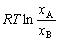 ,且有: ,且有: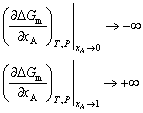 (8-76) (8-76)因此,对于一般二元溶液的两组成端足够小区域内自由能曲线总是呈下凹,如图8-71曲线1,并且ΔGm具有负值。这种情况与上述讨论过的理想溶液相类似。 2)非端点区域 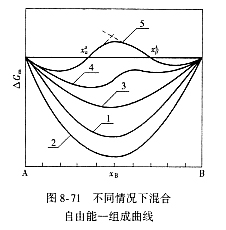 当组成点位于非端点区,自由能-组成曲线变化复杂,它随体系过剩自由能正负和大小的不同而异,但是,为了简单起见,分为如下两种情况来讨论: 当组成点位于非端点区,自由能-组成曲线变化复杂,它随体系过剩自由能正负和大小的不同而异,但是,为了简单起见,分为如下两种情况来讨论:(1)溶液组成γi<1,ΔGmE<0。此时体系出现负偏差。若γi随xi作单调变化,则 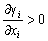 ,二阶导数 ,二阶导数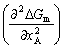 >0。故自由能-组成曲线在整个组成区域内呈下凹(如图8-71中曲线2)。实际混合自由能低于理想混合状态,混合将更有利于体系的稳定。 >0。故自由能-组成曲线在整个组成区域内呈下凹(如图8-71中曲线2)。实际混合自由能低于理想混合状态,混合将更有利于体系的稳定。(2)溶液组成γi>1,ΔGmE>0。此时,体系出现正偏差。若γi随xi作单调变化,则 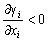 ,二阶导数 ,二阶导数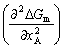 <0依 <0依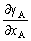 数值大小可取正值或负值。由式(8-75)可知: 数值大小可取正值或负值。由式(8-75)可知:当 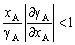 ,则 ,则 ,故自由能-组成曲线仍呈下凹,但是此时实际混合自由能将高于理想混合状态,如图8-71中曲线3。 ,故自由能-组成曲线仍呈下凹,但是此时实际混合自由能将高于理想混合状态,如图8-71中曲线3。当 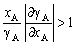 ,则 ,则 ,自由能-组成曲线将在某一组成区间呈现上凸,如图8-71中曲线4。不难理解这种上凸程度随正偏离程度增大而增大。当 ,自由能-组成曲线将在某一组成区间呈现上凸,如图8-71中曲线4。不难理解这种上凸程度随正偏离程度增大而增大。当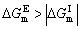 时,实际混合自由能在相应组成区间甚至出现正值,如图8-71中曲线5。此时整个自由能-组成曲线可分成两支:左边分支表明B可溶解于A中形成有限固溶体α相,极限组成为xα5,因为当xα5>xα将导致ΔGm>0的不可能过程。同理,右边的分支表明A可溶解于B中形成有限固溶体β相,其极限组成为xβ5。 时,实际混合自由能在相应组成区间甚至出现正值,如图8-71中曲线5。此时整个自由能-组成曲线可分成两支:左边分支表明B可溶解于A中形成有限固溶体α相,极限组成为xα5,因为当xα5>xα将导致ΔGm>0的不可能过程。同理,右边的分支表明A可溶解于B中形成有限固溶体β相,其极限组成为xβ5。对于自由能-组成曲线图8-71中曲线4的情况,尽管系统混合自由能在整个组成区域中均有ΔGm<0,但在曲线上凸部分的组成区间上从能量的观点来看,任一组成的单相溶液都处于一种亚稳状态。体系组成的区域性热扰动会促使其分解成两相。如图8-72所示,组成为x的溶液,其自由能为W,若该溶液分解为组成为d和e的两个溶液,其自由能分别为M、N。此时系统总自由能为两溶液自由能之和,由杠杆原理可知:总自由能落于图中D点。显然,依此原理进一步的分解将更有利于系统自由能的降低,直至此两相达到平衡,即化学位相等。此时两相自由能分别处于E、F点,它们由两下凹曲线分支的公切线决定,对应的相组成点为y和z,系统的总自由能为G,此时体系最为稳定,能量最低。由此可见,当系统自由能曲线出现上凸时,单一溶液自由能-组成曲线在客观上相当于两种溶液的曲线叠加而成,它们之间存在一不可混溶区,这便是由E、F点所确定的自由能-组成曲线上凸部分相应的组成区域。 |
版权所有 民众工作室.制作 |