
 |
第8章 相平衡与相图 |
| 8.5 相图热力学基本原理(2) 2. 纯物质的化学位等于该物质的摩尔自由能 在物理化学课程中我们已经学过, 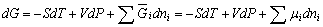 (8-44) (8-44)恒温恒压下,上式变为: 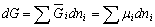 (8-45) (8-45)将上式积分,考虑纯物质特性,则可得: G=μn (8-46) 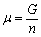 (8-47) (8-47)即纯物质的化学位等于摩尔自由能。 3. 化学位在多相平衡中的应用 假设某一体系在一定温度、压力下,α和β两相处于平衡,根据物理化学知识,有: 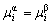 (8-48) (8-48)即多种物质的多相体系处于平衡状态时,除体系各相的温度和压力相同外,各物质在各相中的化学位也必须相等。若系统中有ρ个相,则有: 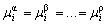 (8-49) (8-49)8.5.2 多相系统中自由能和组成的关系 1. 机械混合物的自由能-组成关系 若有两种物质A和B混在一起没有任何反应即称为机械混合物。这种情况下,若ΔH=0,ΔS=0,则: 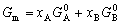 (8-50) (8-50)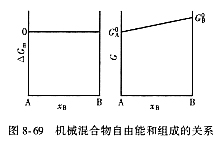 式中,Gm为混合物的自由能, 式中,Gm为混合物的自由能,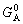 、 、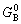 分别是纯物质A、B的摩尔自由能,xA、xB 分别是它们的摩尔分数,xA+xB=1。 分别是纯物质A、B的摩尔自由能,xA、xB 分别是它们的摩尔分数,xA+xB=1。设混合前后自由能变化为 ,因混合前后总自由能不变,即ΔGm,如图8-69。用自由能Gm 和组成关系表示 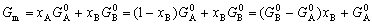 (8-51) (8-51)上式为直线方程,如图8-69所示。当xB=0时,Gm= 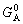 ;当xB=1时,Gm=Gm0. ;当xB=1时,Gm=Gm0.2. 理想溶液自由能-组成曲线 假设A和B两种纯物质混合成理想溶液(把连续固溶体看成属于理想溶液的范畴),它们的摩尔分数分别为 xA、xB , xA+xB=1。均匀混合后,ΔHm=0(混合热为0),但存在混合熵,ΔSm≠ 0。因此,生成理想溶液的反应用下式表示: 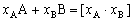 (8-52) (8-52)反应的自由能变化为ΔGm,称为理想溶液生成自由能,即有: 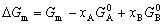 (8-53) (8-53)式中, 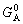 、 、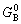 分别是标准状态下纯物质A、B的摩尔自由能,恒温恒压下为常数。Gm为理想溶液的摩尔自由能。已知 分别是标准状态下纯物质A、B的摩尔自由能,恒温恒压下为常数。Gm为理想溶液的摩尔自由能。已知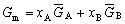 ,代入上式,得: ,代入上式,得: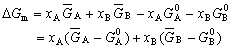 (8-54) (8-54)因为 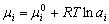 , ,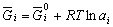 (8-55) (8-55)所以?? 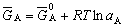 (8-56) (8-56)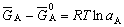 (8-57) (8-57)同理, 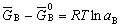 (8-58) (8-58)把上两式代入式(8-54),得: 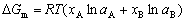 (8-59) (8-59)对理想溶液,aA=xA,aB=xB 则 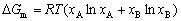 (8-60) (8-60)又因为理想混合时,ΔHm=0 所以 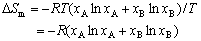 (8-61) (8-61)从式(8-60)可以看出,理想溶液的自由能是温度和组成的函数。在每一个确定的温度下都可以做出自由能-组成关系图。 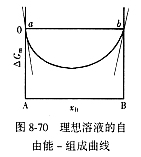 理想溶液自由能-组成曲线是什么形状?现用A-B二元系统为例来说明。横坐标为组成轴,xB=0,xA=1表示纯物质A,这时ΔGmA=0;xA=0,xB=1表示纯物质B,这时ΔGmB=0。如图8-70所示,分别用a、b两点表示ΔGmA和ΔGmB。将式(8-60)作适当变换得: 理想溶液自由能-组成曲线是什么形状?现用A-B二元系统为例来说明。横坐标为组成轴,xB=0,xA=1表示纯物质A,这时ΔGmA=0;xA=0,xB=1表示纯物质B,这时ΔGmB=0。如图8-70所示,分别用a、b两点表示ΔGmA和ΔGmB。将式(8-60)作适当变换得: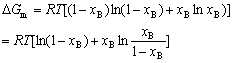 (8-62) (8-62)恒温恒压时,将ΔGm对xB微分并整理得到: 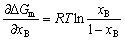 (8-63) (8-63)当A中含微量B时,xB→0,(1-xB)→1,组成点落在组成轴的左端,这时上式变为: 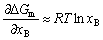 (8-64) (8-64)当xB→0,lnxB→-∞。因此,xB足够小时, 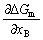 是常负值,即曲线斜率为负值,曲线从左端起是下凹形的。 是常负值,即曲线斜率为负值,曲线从左端起是下凹形的。同样,B中含微量A时,xB→1,(1-xB)→0,组成点落在组成轴的右端,这时式(8-63)变为:  (8-65) (8-65)当xB→1, 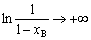 。因此,xA足够小时, 。因此,xA足够小时,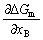 是常正值,即曲线斜率为正,曲线从右端起是下凹形的。 是常正值,即曲线斜率为正,曲线从右端起是下凹形的。从上面分析可看出,在整个组成范围内,理想溶液(固溶体)的自由能-组成曲线是一条下凹形曲线。这也说明,任何纯组分在热力学上并不是最稳定态,纯组分中含有少量第二组分时,可使体系的自由能下降。因此,纯物质在一定环境中总有通过吸附等途径,自发被“污染”的趋势。 |
版权所有 民众工作室.制作 |