| 6.2 固体的表面(2)
6.2.2 固体的表面能
固体的表面能可以通过实验测定或理论计算来确定。较普遍采用的实验方法是将固体熔化测定液态表面张力与温度的关系,作图外推到凝固点以下来估算固体的表面张力。理论计算比较复杂,下面介绍几种近似的理论计算方法。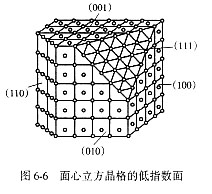
(1)金属的表面能
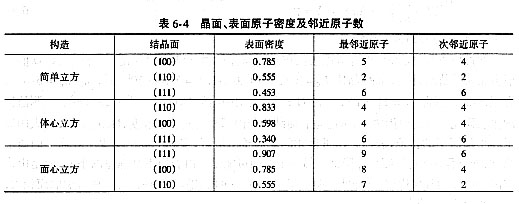
固体表面上的原子只有一侧存在近邻,因此表面上原子的近邻数会比内部的原子少。例如,面心立方结构(图6-6)体内原子的近邻数为12,对(111)、(100)、(110) 面,则每个表面原子的近邻数分别减少3、4和5个,即最近邻数为9、8和7。不同结构晶面上原子近邻数列于表6-4。
因为键合能是负值,表面上的原子将由于邻近键数的减少而增高其能量,比表面能的增量可表示为:
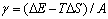 (6-2) (6-2)
0K时T△S为0,由此可以根据材料的摩尔升华热Ls来估算0K时的比表面能γ0。如果采用简单的键合模型(只考虑最近邻间的相互作用),设每对原子键能为?,晶体的配位数为z,阿伏加德罗数为NA,则:
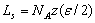 (6-3) (6-3)
要产生两个表面,需要拆开相应的原子键,设形成一个表面原子所需要拆开的键数为zo,原子间距为a,则有:
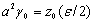 (6-4) (6-4)
考虑到摩尔体积Vm = NAa3,即可根据上两式得出:
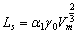 (6-5) (6-5)
其中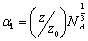 ,对简单立方晶体(100)面,z/zo = 6/1,对面心立方结构的(111)面,z/zo=12/3。式6-5说明,对某一晶体来说,zo越大的表面,越具有较高的比表面能。在较高温度时还需要考虑表面熵,因熵值为正,故有γ<ΔE/A。 ,对简单立方晶体(100)面,z/zo = 6/1,对面心立方结构的(111)面,z/zo=12/3。式6-5说明,对某一晶体来说,zo越大的表面,越具有较高的比表面能。在较高温度时还需要考虑表面熵,因熵值为正,故有γ<ΔE/A。
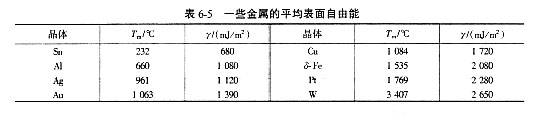
研究已经得出,高熔点金属具有较高的Ls及高的表面能,如表6-5所示。
(2)共价晶体表面能
共价晶体不需考虑长程力的作用,表面能(us)即是破坏单位面积上的全部键所需能量之一半:
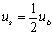 (6-6) (6-6)
式中:ub为破坏化学键所需能量。
以金刚石的表面能计算为例,若解理面平行于(111)面,可以算出每m2上有1.83×1019个键,若取键能为376.6kJ/mol,则可算出表面能为:
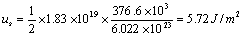
(3) 离子晶体的表面能
取真空和绝对零度的条件,计算晶体中一个离子移到晶体表面时自由能的变化。在0K时,这个变化等于一个离子在这两种状态下的内能差(△u)S,V。以uib和uis分别表示第i个离子在晶内和在表面上时与最邻近离子的作用能,用nib和nis分别表示第i个离子在晶内和表面上的最邻近离子的配位数,则晶内中每取走一个离子所需能量为uib·nib/2,在晶体表面则为nis·uis/2。因为nib>nis而uib≈uis,所以从晶体内取走一个离子比从晶体表面取走一个离子所需能量大。设uib=uis,我们得到第i个离子在体内和表面上两个不同状态下内能差为:
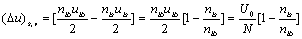 (6-7) (6-7)
U0为晶格能,N为阿伏加德罗常数。如果X表示1m2表面上的离子数,我们从(6-7)式得到:
 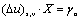 (6-8) (6-8)
其中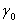 就是0K时的表面能。 就是0K时的表面能。
在推导方程(6-8)时,我们没有考虑表面层结构与晶体内部结构的变化。实际上,计算值一般会比实验值高,例如MgO晶体U0 = 3.93×103J/mol,X=2.26×1019/m2, nis/nib = 5/6,由方程(6-8)计算得 =24.5J/m2。在77K下,真空中测得MgO的 为1.28J/m2。实测值比理想表面能值低的原因之一可能是表面结构与内部相比发生了改变,MgO晶体具有大阴离子和小阳离子的特征,表面将由可极化的氧离子所屏蔽,实际上等于减少了表面上的离子数,根据方程(6-8)就导致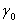 降低。另一个原因可能是自由表面不是理想的平面,而是由许多离子尺度的阶梯构成,这样使实验数据中的真实面积实际上比理伦计算所考虑的面积大,这也使计算 偏大。 降低。另一个原因可能是自由表面不是理想的平面,而是由许多离子尺度的阶梯构成,这样使实验数据中的真实面积实际上比理伦计算所考虑的面积大,这也使计算 偏大。
固体和液体的表面能与周围环境条件,如温度、气压、第二相的性质等条件有关。随着温度上升,表面能下降。一些物质在真空或惰性气体中的表面能列于表6-6。

|

