| 3.3 晶体场理论和配位场理论(1)
3.3.1 晶体场理论的基本概念
晶体场理论是一种推广了的离子成键模式。虽然它仍属于静电理论的范畴,但能够阐明在一系列过渡元素化合物晶格中,用经典的静电理论所无法解释的许多现象。
晶体场理论认为,晶体结构中的每个阳离子都处于一个晶体场之中。所谓晶体场是指晶格中由阳离子配位多面体——与阳离子配位的阴离子或负极朝向中心阳离子的偶极分子——所形成的一个静电势场,中心阳离子就处于该势场之中。认为中心阳离子与周围配位体之间只存在纯粹的静电相互作用,且配位体都被作为点电荷来看待。
已知过渡元素离子的核外电子排布为:
……(n-1)s2(n-1)p6(n-1)d0-10
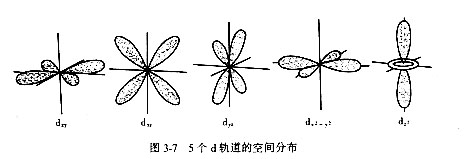
其特点是一般具有未填满的d电子层。d电子层中有五个d轨道,它们的电子云在空间的分布如图3-7所示,其中dx2-y2和dz2轨道沿坐标轴方向伸展;dxy、dxz、dyz轨道则沿坐标轴的对角线方向伸展。每个轨道都可容纳自旋相反的一对电子。因此当五个d轨道全填满时,其电子云在空间叠合呈Oh对称(即m3m对称)。但是当d电子层的电子未填满时,它们的叠合一般不符合Oh对称(半满时除外)。
对于一个过渡元素离子,当它处于球形对称的势场中时,五个d轨道具有相同的能量,即是所谓五重简并的。电子占据任一轨道的几率均相同,但按洪特规则分布,亦即在等价轨道(能量状态相同的轨道)上排布的电子,将尽可能分占不同的轨道,且自旋平行,以便使整个体系处于最低的能量状态。
但是,与通常的极化效应有所不同,当一个过渡元素离子进入晶格中的配位位置时,亦即处于一个晶体场中时,它与周围的配位体相互作用的结果,一方面是过渡元素离子本身的电子层结构将受到配位体的影响而发生变化,使得原来能量状态相同的五个d轨道发生分裂,导致部分d轨道的能量状态降低而另外部分d轨道的能量状态升高,其分裂的具体情况将随晶体场的性质——配位体的种类和配位多面体形状的不同而异。另一方面,配位体的配置也将受到中心过渡元素离子的影响而发生变化,引起配位多面体的畸变。在一般情况下,周围配位体对中心过渡元素离子的影响是主要的,相反的影响只在某些离子的情况下才较为显著。
3.3.2 d轨道的晶体场分裂
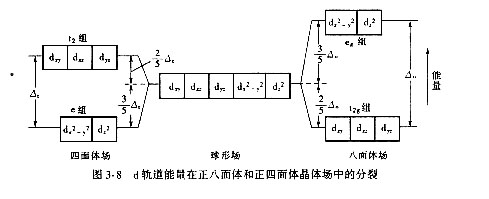
首先考虑一个过渡元素离子在正八面体晶体场中的情况。当六个带负电荷的配位体(例如O2-等阴离子或者H2O等偶极分子的负端)分别沿三个坐标轴 ±x、±y和±z方向向中心过渡金属阳离子接近,最终形成正八面体配合物时,中心离子沿坐标轴方向伸展的dz2和dx2-y2轨道便与配位体处于迎头相碰的位置,这两个轨道上的电子,将受到带负电荷的配位体的排斥作用,因而能量增高;而沿着坐标轴对角线方向伸展的dxy、dxz和dyz轨道,它们因正好插入配位体的间隙之中,因而能量较低。这样,原来能量相等的五个d轨道,在晶体场中便分裂成为两组:一组是能量较高的dz2和dx2-y2轨道组,称为eg组轨道;另一组是能量较低的dxy、dxz和dyz轨道组,称为t2g组轨道。对于晶格中位于配位八面体中的过渡金属离子来说,它所处的情况就是如图3-8所示。过渡元素离子中原来是五重简并的d轨道,在晶体场中发生能量上的变化而分裂的现象,称为晶体场分裂。
eg轨道中的每个电子所具有的能量E(eg)与t2g轨道中每个电子的能量E(t2g)两者的差,称为晶体场分裂参数。在正八面体场中,将它记为Δo。
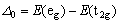 (3-13) (3-13)
d轨道在晶体场中能量上的分离,服从于所谓的“重心”规则,亦即d轨道在晶体场的作用下发生分裂的过程中,其总能量保持不变。如果以未分裂时d轨道的能量,也就是说以离子处于球形场中时d轨道的能量作为0(由于晶体场理论只涉及到能量相对大小的问题,因此完全可以不必考虑其绝对能量值到底是多少),则应有:
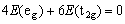 (3-14) (3-14)
由(3-13)和(3-14)式可得:
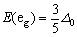 , , 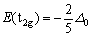 (3-15) (3-15)
如果过渡元素离子不是处于八面体场中而是在一个四面体配位的晶体场中,此时dz2和dx2-y2轨道恰好插入配位体的间隙之中,而dxy、dxz、dyz轨道与配位体靠得较近,结果产生了与正八面体晶体场中的能量状态正好相反的变化,即dxy、dxz、dyz三个轨道(此时称为t2组轨道)能量增高,而dz2和dx2-y2两个轨道(称为e组轨道)能量降低(图3-8)。记相应的晶体场分裂参数为Δt,则有:
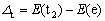 (3-16) (3-16)
式中的E(t2)和E(e)分别为t2组轨道和e组轨道中电子的能量。同样,根据“重心”规则得到:
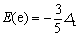 , ,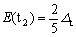 (3-17) (3-17)
根据静电模型的量子学计算表明:
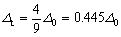 (3-18) (3-18)
实际晶体中阳离子位置的对称性,或者说它的配位多面体的对称性,往往低于正八面体或正四面体的对称性。在这样的晶体场中,原来是五重简并的五个d轨道,在能量上可以分裂成为三组、四组乃至五组彼此分开的轨道。
|

