| 3.1 结合键(3)
3.1.3 金属键
金属是重要的固体材料之一,在109种化学元素中,金属约占80%。金属的共同性质是:不透明,有金属光泽,有良好的导热性、导电性和延展性。金属所表现出的这些特性与金属键密切相关。
对金属键的解释目前存在2种理论,即“自由电子”模型和能带理论。“自由电子”模型认为金属元素的电负性小,电离能也小,外层价电子很容易摆脱原子核的束缚而成为“自由电子”,并在失去电子的金属正离子按紧密堆积方式构成的晶格势场中自由运动。这些“自由电子”在三维空间中运动,离域范围很大,为所有金属原子所共有。这种金属正离子与自由电子之间的相互作用就构成了金属原子间的结合力——金属键。应用这个模型可以很好解释金属材料的一些特性,如金属具有高导电性和导热性,自由电子能吸收光波能量,产生跃迁,从而表现出有金属光泽、不透明。另外,金属正离子以球形密堆积方式组成,晶体原子间可滑动,表现出有延展性,并说明金属键没有方向性和饱和性。
“自由电子”模型在解释一些金属导电性和比热容等方面也暴露了一些不足,这主要是忽视了电子间的相互作用,从而出现偏差。要更深入地认识金属键的本质,固体的能带理论可得出较好的解释。有关固体能带理论将在固体物理等相关课程中学习。
通过上面讨论,我们可以认为金属键是多原子共价键的极限情况,是考虑了电子的波动性以及金属正离子的点阵势能场以及电子与电子、电子与点阵的相互作用而得出来的,电子共有化程度显著,形成能带结构的特殊结果。
3.1.4 范德华键
除了离子键、共价键和金属键外,材料中分子之间还存在较弱的分子间作用力,范德华键就是其中一种。范德华键的键能比其他化学键的键能低约1~2个数量级,作用范围约为0.3~0.5 nm,没有方向性和饱和性。范德华力与距离r满足1/r7的正比例函数关系,它主要源自以下3种力。
1.静电力
很多极性分子正、负电荷中心不重合,具有永久偶极矩,一个分子的偶极矩正端与邻近另一个分子偶极矩负端产生静电吸引。静电力即偶极子与偶极子之间的作用力,偶极子之间的静电吸引能为
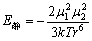 (3-7) (3-7)
式中,μ12和μ22分别是两个相互作用分子的偶极矩;r是偶极子之间的质心距离;k是为波尔兹曼常数;T为绝对温度。μi=eli(i=1,2),e为电荷,l为正负电荷中心距。从式(3-7)可看出,偶极矩越大,静电力越大。当温度升高时,相互作用能减少,这是因为随着温度的升高,分子热运动加剧,扰乱了偶极矩的取向,削弱了静电吸引力。
2.诱导力
一般认为,非极性分子没有偶极矩,正负电荷中心是重合的。但在极性分子与非极性分子组成的体系中,当非极性分子与极性分子靠近时,受到极性分子偶极电场的作用而使正负电荷位移,正负电荷中心不再重合,被诱发产生一个诱导偶极矩,该诱导偶极矩与极性分子的偶极矩之间发生静电作用,二者之间的作用力就是诱导力。其相互作用能为
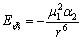 (3-8) (3-8)
式中,μ12为极性分子的偶极矩;a2为诱导偶极子的极化率。可见诱导力与极性分子偶极矩和诱导偶极子极化率大小有关。
.jpg)
|

