6.3 界面结构(4)

    6.3.5 晶界结构模型

    （1）重合位置点阵(CSL)模型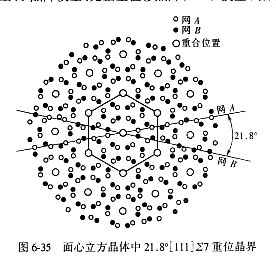
    重位点阵又称相符点阵，如图6-35所示。图中假定在面心立方晶体中两相邻的平行晶面绕[111]轴相对旋转21.8°，网A和网B在(111)面上的原子排列分别以小空心圆和小实心圆表示，相对旋转后位于两个网上的重合位以大空心圆表示，可以看到，这些重合位也构成了一个相似于网A或网B的六角形网，但原子间距变大。通过直接查数已确定出重合位的数量是网A或网B的1／7，该值称为重合位密度，其倒数称为倒易密度，用希腊字母Σ表示。
    重位点阵可以用4个基本参数来描述，即旋转轴[hkl]；绕轴的旋转角θ；重位网上的一个重合点在（hkl）面上的坐标(x，y)；倒易密度Σ（最小奇数）。这4个参数并不是完全独立的，存在下列的关系：
                  (6-54)
                                                    (6-55)
                                                 (6-56)
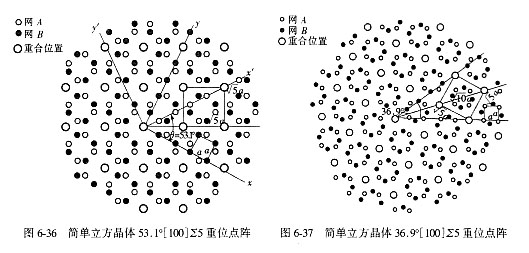
    现举例说明上述关系式的应用。考虑一个简单立方点阵绕[100] 轴旋转的情况，如图6-36所示。图中为(100)平面，x和y轴分别为[010]和[001]，轴单位是简单立方晶胞的边长。点阵绕[100]旋转一角度 后，x、y轴分别占据x′、y′轴位置。因为旋转轴是[100]，得N =1。若取x = 2，y = l就可以得到 = 2arctan(1／2)  = 53.1°， =22+12(1) = 5的一个重位点阵。在图6-36中，x、y坐标下的原子是实心圆，x′、y′坐标对应的原子是空心圆，重位是大空心圆。由此看出重位点阵的晶胞在(100)面上的边长为 ，a是原点阵的点阵常数。
    如果取x=3，y=1，旋转轴仍是[100]，就会得到另一个重位点阵，如图6-37所示。此时 = 2arctan(1／3)  = 36.9°，Σ=32+12(1)=10，在立方点阵中Σ只能取奇数，因此Σ的正确值是10÷2 = 5。这一点阵与x = 2，y = 1的重位点阵是相同的。由此可看出，同一点阵可以通过旋转53.1°或36.9°得到，二角之和为90°。这一结果与立方晶系[100]轴的四次对称有关。