6.3 界面结构(2)

    （4）小角晶界晶界能
    按照小角晶界结构的位错模型，相应的界面能应是晶界上所有位错的总能量。对简单倾转晶界，界面能是一系列同号位错产生的位错应变能。我们已经知道单位长度的刃位错能量可表达为：
                                          （6-43）
式中：G为剪切模量，b为柏氏矢量，ν为泊松比，Ec为位错中心能量，D为位错间距。设同号刃位错之间不存在在滑移矢量方向上的交互作用，每个位错上方存在压应力，下方存在拉应力，即晶界存在交替的压缩和拉伸区域，在半径为D的圆周以外，位错的应力场彼此抵消，亦即上式中取位错应力场的极限距离为D，对应单位长度上晶界的位错密度为1／D（ = ／b），则晶界单位面积界面能γgb与相应位错能量的关系为：
              （6-44）
或写成                                         （6-45）
式中：   ；   。以γgb/ —ln 作图，直线的斜率即为－γ0，截距为γ0A。然后再以γgb－ 作图，得到的曲线具有 以下几个特点：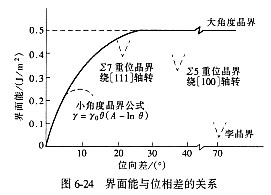
    ① 当 = 0， ln →0，代人式(6-44)得到γgb= 0。
    ② 斜率dγgb／d = γ0(A－1－ln )，若 =0，则斜率为无穷大；随 增加斜率减小。
    ③ 若γgb的最大值(γgb)m对应的 为 ，则有：
                        dγgb/d = 0 = γ0 (A－1－ln )
  = exp(A－1)                          (6-46)
代入式(6-45)得到                        (6-47)
    上式表达了界面能与取向角之间的理论关系。研究表明，所得理论曲线与实验测定吻合的较好。以Cu为例的研究结果示于图6-24，图中也示出了其它晶界模型的取值情况。由图看出，对小角晶界模型，上述关系只能在10°以内符合，超出10°后计算值（虚线）与实验值(实线)不再符合。
    以上公式对扭转晶界也适用，但与位错能相关的系数 和A值会不同。
6.3.3 大角晶界及界面能

    （1）大角晶界
    早期的大角晶界模型是皂泡模型，认为晶界由大约3～4个原子间距厚的区域组成，晶界层内原子排列较差，具有比较松散的结构，原子间的键被打断或被严重扭曲，具有较高的界面能量。此外早期也曾提出另两种模型：一是过冷液体模型，认为晶界层中的原子排列接近于过冷液体或非晶态物质，在应力的作用下可引起粘性流动，但发现只有认为晶界层很薄(不超过两三个原子厚度)时才符合实验结果；第二个模型是小岛模型，认为晶界中存在着原子排列匹配良好的岛屿，散布在排列匹配不好的区域中，这些岛屿的直径约数个原子间距，用小岛模型同样也能解释晶界滑动的现象。
理论上，大角晶界可以分为特殊大角晶界和任意大角晶界两类。特殊大角晶界的能量比任意大角晶界低，亦即当在某些特殊取向角下，晶界上相邻的点阵匹配的较好，此时晶界表现出较低的能态。
    最简单的特殊大角晶界是共格晶界。如果界面上的原子正好位于两晶体的晶格结点上，就形成了共格晶界；当两个晶粒的取向互为对称时，就形成了共格孪晶界，如图6-25(a)所示。对于孪晶界，如果不是精确地平行于孪晶面，如图6-25(b)所示，界面上的原子将不能和它邻接的两个晶粒很好地匹配，这种界面称为非共格孪晶界。
（2）界面能
    大角晶界具有较高的能量，并且基本上不随位向差而改变，见图6-24。关于大角晶界的晶界能 ，研究表明一般实验测得值大约为表面能 的1/3。
    ①任意大角晶界能
    实验上晶界能 一般采用图6-26所示的热蚀法测定，即在高温下长时加热，使之达到平衡状态，然后测定二面角，从下式平衡关系：
γgb-2γcos（θ/2）= 0        (6-48)
得到 。如同表面能一样，γgb的大小也是与结合键的削弱有关，同样可与升华热建立联系，也具有负的温度系数，即随温度的升高γgb是降低的。
    ②特殊大角晶界能
    共格孪晶界：共格孪晶界是一种具有孪晶关系的两个晶体间的对称倾转晶界。由于共格孪晶界的原子基本上处于无畸变的状态，所以相对于任意大角晶界来说，共格孪晶界的能量非常低。图6-24中示出Cu的共格孪晶界能仅为21mJ／m2。
    非共格孪晶界：由于界面上的原子不能很好地和它相邻的两个晶粒匹配，会导致界面能升高。表6-8列出一些晶体晶界能的实验测量值，其中Cu的非共格孪晶界能为498mJ／m2。此外，孪晶界面能对于晶界面的取向非常敏感，若作 与晶界取向的函数关系，在共格孪晶界位置会出现一个尖锐的极小值点（图6-27）。