| 7.1 扩散定律(2)
7.1.3 扩散方程的求解
1. 扩散第一方程
扩散第一方程可直接用于描述稳定扩散过程。下面用氧通过金属薄壁的扩散过程来说明扩散第一方程的解法。
 如图7-3所示,一个内外径分别为r1和r2的球罐中储存有高压氧气,罐内气压为p1,罐外大气中氧分压为p2。由于氧气泄漏非常缓慢,所以假设p1不随时间变化,达到稳态后,氧气将以一恒定速率泄漏。由菲克第一定律,氧气在球罐壁内的扩散通量为 如图7-3所示,一个内外径分别为r1和r2的球罐中储存有高压氧气,罐内气压为p1,罐外大气中氧分压为p2。由于氧气泄漏非常缓慢,所以假设p1不随时间变化,达到稳态后,氧气将以一恒定速率泄漏。由菲克第一定律,氧气在球罐壁内的扩散通量为
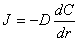
则,通过整个球罐壁单位时间泄漏的氧气量为
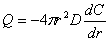 (7-3) (7-3)
对上式积分,有
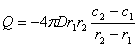 (7-4) (7-4)
其中,c1和c2分别为氧分子在球罐内、外壁的溶解度。根据Sievert定律,双原子分子气体在固体中的溶解度通常与压力的平方根成正比,即c=Kp1/2因此,单位时间内氧气泄漏量为
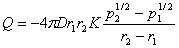 (7-5) (7-5)
2. 扩散第二方程
1)高斯解
把总量为M的扩散元素沉淀成非常薄的薄层,夹在两个“无限”厚的相同试样之间进行扩散。这里的无限厚是指试样的厚度或长度远大于点阵扩散长度时的情况。这时近似取沉淀层的厚度为零,则方程(7-2)的初始条件和边界条件分别为
t=0,x=0 C=∞
x≠0 C=0
t≥0 x=±∞ C=0
满足方程(7-2)及上述条件的解为
 (7-6) (7-6)
此解称为高斯函数解,其曲线如图7-4所示。若沉淀物是置于试样表面的薄层,即扩散只向x>0扩散,则方程的解应为
 (7-7) (7-7)
利用此解可以通过示踪原子法测定固体材料中扩散系数,以及解决半导体掺杂过程中的扩散问题。
|

