| 7.1 扩散定律(1)
7.1.1 菲克第一定律(Fick’s First Law)
扩散过程可以分类为稳态和非稳态。
 在稳态扩散中,单位时间内通过垂直于给定方向的单位面积的净原子数(称为通量)不随时间变化,即任一点的浓度不随时间变化。在非稳态扩散中,通量随时间而变化。研究扩散时首先遇到的是扩散速率问题。 在稳态扩散中,单位时间内通过垂直于给定方向的单位面积的净原子数(称为通量)不随时间变化,即任一点的浓度不随时间变化。在非稳态扩散中,通量随时间而变化。研究扩散时首先遇到的是扩散速率问题。
 菲克(A. Fick)在1855年提出了菲克第一定律,将扩散通量和浓度梯度联系起来。菲克第一定律指出,在稳态扩散(即 )的条件下,单位时间内通过垂直于扩散方向的单位面积的扩散物质量(通称扩散通量)与该截面处的浓度梯度成正比。为简便起见,仅考虑单向扩散问题。设扩散沿x轴方向进行(图7-1),菲克第一定律的表达式为 菲克(A. Fick)在1855年提出了菲克第一定律,将扩散通量和浓度梯度联系起来。菲克第一定律指出,在稳态扩散(即 )的条件下,单位时间内通过垂直于扩散方向的单位面积的扩散物质量(通称扩散通量)与该截面处的浓度梯度成正比。为简便起见,仅考虑单向扩散问题。设扩散沿x轴方向进行(图7-1),菲克第一定律的表达式为
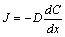 (7-1) (7-1)
式中:J为扩散通量(atoms/(m2·s)或kg/(m2·s));D为扩散系数(m2/s); 为浓度梯度(atoms/(m3·m)或kg/(m3·m)) (图7-2为浓度梯度示意图);“-”号表示扩散方向为浓度梯度的反方向,即扩散由高浓度向低浓度区进行。此方程又称为扩散第一方程。
当扩散在稳态条件下应用(7-1)式相当方便。
7.1.2 菲克第二定律 (Fick’s Second Law)
实际上,大多数重要的扩散是非稳态的,在扩散过程中扩散物质的浓度随时间而变化,即dc/dx≠0。为了研究这种情况,根据扩散物质的质量平衡,在菲克第一定律的基础上推导出了菲克第二定律,用以分析非稳态扩散。在一维情况下,菲克第二定律的表达式为
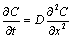 (7-2) (7-2)
式中: 为扩散物质的体积浓度(atoms/m3或kg/m3); 为扩散时间(s); 为扩散距离(m)。
(7-2)式给出c=f(t,x)函数关系。式(7-2)又称为扩散第二方程。由扩散过程的初始条件和边界条件可求出(7-2)式的通解。利用通解可解决包括非稳态扩散的具体扩散问题。
|

