| 第3节 位错(2)
4. 柏氏矢量
为了便于进一步分析位错的特征,同时避免繁琐的原子模型,建立了一个简单的物理参量来描述位错区原子的畸变特征的矢量,称作柏氏矢量。
(1)柏氏矢量的确定方法
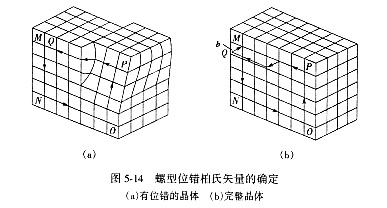
先确定位错的方向(一般规定位错线垂直纸面时,由纸面向外为正),按右手法则做柏氏回路,右手大拇指指位错正方向,回路方向按右手螺旋方向确定。从实际晶体中任一原子M出发,避开位错附近的严重畸变区作一闭合回路 MNOPQ,回路每一步连结相邻原子。按同样方法在完整晶体中做同样回路,步数,方向与上述回路一致,这时终点 Q和起点 M 不重合,由终点Q 到起点M 引一矢量QM 即为柏氏矢量b。柏氏矢量与起点的选择无关,也与路径无关,图5-12、图5-13示出刃型位错与螺型位错柏氏矢量的确定方法及过程。
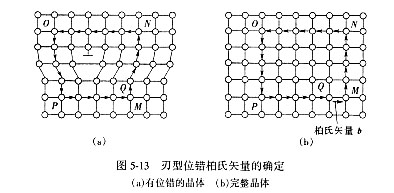
(2)柏氏矢量的物理意义及特征
柏氏矢量是描述位错实质的重要物理量。反映出柏氏回路包含的位错所引起点阵畸变的总累计。通常将柏氏矢量称为位错强度,位错的许多性质如位错的能量,所受的力,应力场,位错反应等均与其有关。它也表示出晶体滑移时原子移动的大小和方向。
柏氏矢量具有守恒性,柏氏回路任意扩大和移动中,只要不与原位错线或其他位错线相遇,回路的畸变总累计不变,由此可引申出一个结论:一根不可分叉的任何形状的位错只有一个柏氏矢量。
利用柏氏矢量b与位错线t的关系,可判定位错类型。若b ∥ t则为螺型位错,其中同向为右螺,反向为左螺,如图5-13。若b ⊥ t为刃型位错,其正负用右手法则判定,右手拇指、食指与中指构成一直角坐标系,以食指指向t方向,中指指向b正方向,则拇指代表多余半原子面方向,多余半原子面在上称正刃型位错,反之称负刃型位错。
5. 晶体中位错的组态和位错密度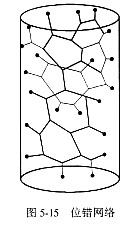
位错在晶体中的分布形式很多。位错在经充分退火的金属中,相互连接成网络,称之为位错网;也可以垂直排列成小角度晶界。经塑性变形的金属中,位错可以在滑移面上形成塞积群;也可能在夹杂物或沉淀物周围形成位错环;也可能形成更复杂的位错缠结等。总之,晶体中位错的组态非常复杂。图5-14是晶体中位错网络的模型。
晶体中的位错数量常用位错密度来表示,位错密度是指单位面积内位错线的总长度。其表达式为
LV=L/V (5-37)
式中:LV是体位错密度;L是位错线的总长度;V是晶体的体积。
但是,由于很难从实验中直接测出位错总长度L;实际上无法直接测定 。为了方便,经常用穿过单位面积的位错数目ρA来表示位错密度。
ρA=n/A
式中,n是穿过截面的位错数;A是截面面积。
位错密度的单位是cm-2。实验结果表明,充分退火后的金属中位错密度约为106~108 cm-2;而经过强烈塑性变形的金属中位错密度可达1010~1012 cm-2。
|

