| 第6节 晶体的堆积方式(2)
对于ABAB……紧密堆积方式,其球体在空间的分布是与空间格子中的六方格子相对应,因此称为六方最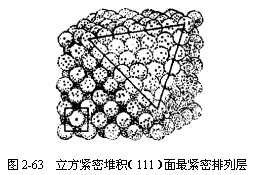 紧密堆积,其最紧密排列层平行于(0001)面。而ABCABC……紧密堆积方式,其球体在空间的分布与空间格子中的立方面心格子相一致,因此称为立方最紧密堆积,其最紧密排列层平行于(111)面(图2-63)。除了上述两种堆积方式外,等大球体还有几种堆积方式,但不是最紧密堆积,如体心立方堆积、简单立方堆积、简单六方堆积、体心四方堆积、四面体堆积等。此外,从上述的球体密堆积方式看,还可能有诸如ABCBABCB……等一系列不同方式,但这在晶体构造中出现很少。六方最紧密堆积和立方最紧密堆积是晶体构造中最常见的两种方式。 紧密堆积,其最紧密排列层平行于(0001)面。而ABCABC……紧密堆积方式,其球体在空间的分布与空间格子中的立方面心格子相一致,因此称为立方最紧密堆积,其最紧密排列层平行于(111)面(图2-63)。除了上述两种堆积方式外,等大球体还有几种堆积方式,但不是最紧密堆积,如体心立方堆积、简单立方堆积、简单六方堆积、体心四方堆积、四面体堆积等。此外,从上述的球体密堆积方式看,还可能有诸如ABCBABCB……等一系列不同方式,但这在晶体构造中出现很少。六方最紧密堆积和立方最紧密堆积是晶体构造中最常见的两种方式。
在上述的等大球体紧密堆积中,存在着两种空隙。一种是处于四个球体包围之中的空隙,四个球体中心之联线恰好成一个四面体的形状,称为四面体空隙。这种空隙就是上面所述的未穿透两层的空隙。另一种是处于六个球体包围之中的空隙,六个球体中心之联线恰好联成一个八面体的形状,称为八面体空隙。这种空隙就是上面所述的连续穿透两层的空隙。显然八面体空隙的空间要大于四面体空隙的空间。
现在来考察一下紧密堆积中球数和两种空隙数之间的关系。分析图2-61中任一球周围的情况得出,在该球下面有紧靠它的3个八面体空隙和4个四面体空隙。如果按六方紧密堆积考虑,第三层和第一层相同,那么在该球的上部也有紧靠它的3个八面体空隙和4个四面体空隙。于是在六方紧密堆积中,每一个球的周围共有6个八面体空隙和8个四面体空隙,而八面体空隙是由6个球共有,四面体空隙由4个球共有,因此属于一个球体的八面体空隙和四面体空隙应为6×1/6 = 1个八面体空隙和8×1/4 = 2个四面体空隙。于是可以得出推广结论,若有n个等大球体作最紧密堆积,将有n个八面体空隙和2n个四面体空隙存在。对于ABCABC……型的立方紧密堆积,这一结果同样正确。
(2)不等大球体的紧密堆积
对不等大球体堆积,可以看成较大的球体作等大球体的最紧密堆积,较小的球按其本身的大小,充填在八面体或四面体空隙中,形成不等大球体的紧密堆积。这种堆积方式,在离子晶体构造中相当于半径较大的阴离子作最紧密堆积,半径较小的阳离子充填于空隙中。在实际晶体构造中,阳离子的大小不一定能无间隙地充填在空隙中,往往是阳离子的尺寸稍大于空隙,而将阴离子略微“撑开”。相反,在某些晶体构造中,阳离子的尺寸较小,填充在阴离子形成的空隙内可以有一定的位移。这两种结果都将可能导致阴离子近似地做最紧密堆积或出现某种程度的变形。
(本节完,本章完)
|

