第3节 晶体的理想形态(1)

     2.3.1单形

    （1） 单形的概念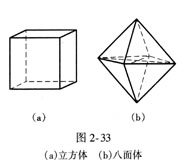
    单形是由对称要素联系起来的一组晶面的总和。即单形是由一个初始晶面经点群中全部对称要素的操作而重复出的一组晶面。因此，同一单形的晶面同形等大。如图2-33中的立方体和八面体，它们的一组晶面分别是同形等大的6个正方形和8个等边三角形。
    （2）单形的推导
    在同一点群中，初始晶面与对称要素的相对位置不同，可以导出不同的单形。对晶体32个点群逐一进行推导可以得到晶体所有的单形。
以L²2P点群为例推导单形，其对称要素在空间的分布如图2-34。初始晶面与对称要素的相对位置有5种(图2-35)：
    ①位置1(图2-35a)：初始晶面垂直L²和2P，通过L2和2P的操作不能产生新的晶面，这一晶面就构成了一个单面单形。
    ②位置2(图2-35b)：初始晶面平行L²和其中一个对称面P₂，并垂直另一个对称面P₁。通过L²和P₂的操作可产生另一平行它的晶面，构成了一个平行双面单形。
            

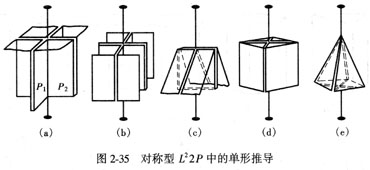
    ③位置3(图2-35c)：初始晶面与L²及P₂斜交，并与P₁垂直。L²和P₂的作用可以产生一个与初始晶面相交的晶面，这两个晶面组成一个双面单形。
    ④位置4(图2-35d)：初始晶面与L²平行，而与2P斜交。通过2P或通过P与L²的作用可获得平行L²的四个晶面，它们组成一个斜方柱单形。   
    ⑤位置5(图2-35e)：初始晶面与L²及2P斜交。通过2P或L²与P的作用可获得相交于一个顶点的四个晶面，它们组成一个斜方单锥单形。
    对每一种点群，初始晶面与对称要素的相对位置最多只可能有7种。因此同一点群中，最多能导出七种单形。对于那些对称要素较少的点群来说，晶面与对称要素可能的相对位置数还会减少。这样，对32种点群逐个进行推导，去掉形态重复的单形，共得到47种，统称为几何单形。   
    如果不仅考虑几何形态的不同，同时还考虑点群的类型，则单形共有146种，称为结晶单形。即在这146种结晶单形中，有些单形同属于一种几何单形。