2.2 流动液体的力学规律
◆基本概念
◆连续性方程
◆伯努利方程
2.2.1 基本概念
◆理想液体: 既不可压缩又无粘性的液体。
◆理想气体: 可压缩但没有粘性的气体。
◆一维定常流动: 即流场中速度与压力只是空间点的位置的函数而与时间无关,则称流场中的流动为定常流动。在定常流动条件下,如果通过适当选择坐标(包括曲线坐标)后,使流速与压力只是一个坐标的函数,则称这样的流动为一维定常流动。
◆通流截面:在流场中作一面。若该面与通过面上的每一条流线都垂直,则称该面为通流截面。
 图2—7 流线、流束与通流截面 图2—7 流线、流束与通流截面
◆流量:单位时间内流过某通流截面的流体体积。
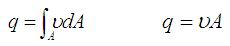
法定单位: 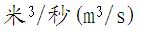 ,工程中常用升/分(L/min) ,工程中常用升/分(L/min)
◆通流截面上的平均流速:
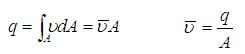
◆流动液体中的压力和能量: 由于存在运动,所以理想流体流动时除了具有压力能与位能外,还具有动能。即流动理想流体具有压力能,位能和动能三种能量形式.
单位重量的压力能: 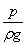
单位重量的位能: Z .
单位重量的动能: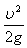
2.2.2 连续性方程:
质量守恒定律在流动液体情况下的具体应用.
◆q=vA=常数
◆不可压缩流体作定常流动时,通过流束(或管道)的任一通流截面的流量相等.
◆通过通流截面的流速则与通流截面的面积成反比.
2.2.3 伯努利方程(能量方程):
能量守恒定律在流动液体中的表达形式
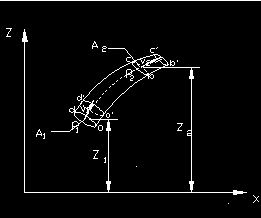 图2-8 伯努利方程推导意简图 图2-8 伯努利方程推导意简图
◇理想液体的伯努利方程
◇实际液体的伯努利方程
◇伯努利方程应用实例
◆理想液体的伯努利方程
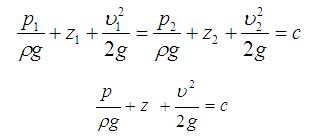
理想液体定常流动时,液体的任一通流截面上的总比能(单位重量液体的总能量)保持为定值。
总比能由比压能(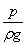 )、比位能(Z)和比动能( )、比位能(Z)和比动能(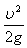 )组成,可以相互转化。 )组成,可以相互转化。
由于方程中的每一项均以长度为量纲,所以亦分别称为压力水头,位置水头和速度水头.
静压力基本方程是伯努利方程的特例.
◆实际液体的伯努利方程
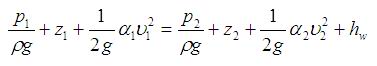
α:动能修正系数,为截面上单位时间内流过液体所具有的实际动能,与按截面上平均流速计算的动能之比(层流时α=2,紊流时α=1)
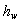 :单位重量液体所消耗的能量 :单位重量液体所消耗的能量
◆伯努利方程应用实例
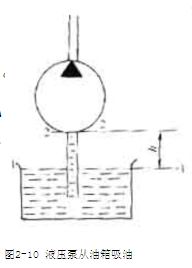
液压泵吸油口处的真空度是油箱液面压力与吸油口处压力p2之差。
液压泵吸油口处的真空度却不能太大. 实践中一般要求液压泵的吸油口的高度h不超过0.5米.
|

